Evaluation on the river seepage under groundwater pumping near riverside

Jung-Wei Chen1,a Kuan-Wei Chen2,b Jung-Nan Chang3,c Sun-Zone Lee4,d Cheng-Haw Lee5*,e

1 Institute of Hot Spring Industry, Chia Nan University of Pharmacy & Science, 60, Erh-Jen RD.,Sec.1, Jen-Te, Tainan 71710, Taiwan

2 Department of Tourism Management, Chia Nan University of Pharmacy & Science, 60, Erh-Jen RD.,Sec.1, Jen-Te, Tainan 71710, Taiwan<

3 Department of Civil Engineering and Institute of Civil Engineering Technology, National KaohsiungUniversity of Applied Sciences, No.415, Chien Kung Rd., Kaohsiung 807, Taiwan

4 Department of Environmental Engineering & Science, Chia Nan University of Pharmacy & Science,60, Erh-Jen RD., Sec.1, Jen-Te, Tainan 71710, Taiwan

5 Department of Resources Engineering, National Cheng Kung University, No.1, Dasyue Rd., East District, Tainan City 70101, Taiwan

acjw2623@mail.chna.edu.tw, bckw0814@mail.chna.edu.tw, ct0910715493@yahoo.com.tw,

dmszlee@mail.chna.edu.tw, eLeech@mail.ncku.edu.tw

Keywords: groundwater, riverbank filtration, river seepage, groundwater radius of influence Abstract. Groundwater is to be pumping near the riverside could be induced recharge from the river Owing to the precipitous terrain of Taiwan, its rivers are short and most rainwater flows into the ocean through the ground. There are not enough accessible water resources and the people currently obtain their water form the groundwater. However, the land subsidence is a serious problem in Taiwan coastal area because of groundwater over-pumping. If water is to be pumping from the riverside areas, it may be intercepted indirectly from the river. The aquifer can recharge from the river and lateral groundwater flow, and could be reduced the negative effect on the aquifer. There is no reservoir or lakes to storage water facility in the Zhanghua area of middle Taiwan, thus the water used by the people and the industries all come from groundwater and external water sources. For increase the water supply of the Zhanghua area, this research proposes the mode of obtaining groundwater from the riverside and assesses the effect of this method on the river seepage.
The analytical model was introduced by Theis (1941) and Glover and Balmer (1954) in unconfined aquifers[11,21]. In this situation, the river fully penetrates the aquifer and the groundwater gets through a fully penetrating pumping well. The overlapping theory is then used to deduce the ratio of the river seepage to pumping. Hantush (1965) and Jenkins (1968) made a hypothesis that if there is a low permeable soil layer in the system of rivers and aquifer, this will result in an incomplete connection between the rivers and aquifer[13,16]. Grigoryev (1957) and Bochever (1966) estimated the river seepage that resulted from getting groundwater from the riverside when the river partially penetrates the aquifer[2,12].
Wilson (1993) proposed an analytical formula to analyze the effect of boundary conditions on the river seepage when groundwater is obtained from the riverside[23]. Moreover, by adopting the analytical solution of Hantush (1965), Hunt (1999) estimated the river seepage and proposed an analytic solution for lowering of the groundwater level at each point in the aquifer under the circumstances that the river partially penetrates the aquifer and hade low permeability of riverbed[13,15]. Chen and Chen (2003) studied the hydraulic gradient change caused by pumping the groundwater, inducing the river seepage to the well and recharge the aquifer[10]. The particle tracking model was applied to describe the process of the river moving to the part of the penetrating well in the aquifer with anisotropy. Then, by using the analytical solution proposed by Hunt (1999), Chen and Yin (2004) estimated the river seepage and basic flow decrement of a river that resulted from pumping according to the recharge mode of aquifer to the river when the water level difference is known[9,15]. Chen et al. (2009) to estimate the stream infiltration with consideration to the variation of the river water level by Ferris analytical model, stream-flow estimation model and the groundwater flow numerical software MODFLOW[7]. The results indicate that an increasing efficiency of river seepage is within the range of 10.0% to 18.5% in the Hsinhuwei River, Taiwan.
Generally, the numerical method is used to study the relatively complicated situations that are related to the groundwater and the river, including the river that partially penetrates the aquifer, the partially penetrating well, the anisotropic aquifer, and the irregular riverbed, among others. Butler et al. (2001) divided the aquifer into seven layers by using the groundwater numerical software of MODFLOW, and its analog results were consistent with the analytical resolution proposed byGlover and Balmer in 1954[3]. Lastly, Matteo and Dragoni (2005) constructed a hydrogeologic model by using MODFLOW[18]. Different the research made by Bulter et al. (2001), they took the lateral recharge of the aquifer and the distance between the top well screen and riverbed into account, and proposed an empirical formula for getting ground water from the anisotropic aquifer.
This research constructed a numerical model for riverside groundwater pumping based on the parameters estimated from the field experiments (Hsieh et al., 2007)[14], estimated the optimal pumping of single well near the riverside, proposed five groundwater pumping schemes according to the number of different wells, pumping of wells, and made an assessment on the effect of each scheme on the groundwater byMODFLOW.

2 General description of the research area

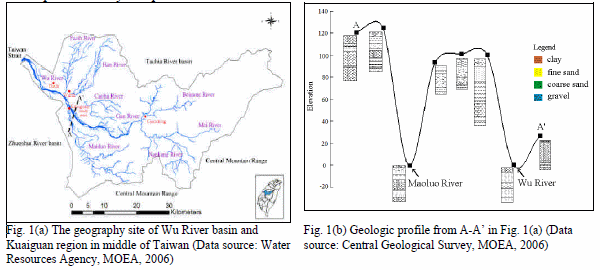
Most of the water used daily by individuals and industries in the Zhanghua region of middle Taiwan comes from groundwater resources. At present, it still relies on the complement from the other water source, thus it is rather short of water supply. Consequently, this research proposes a riverside groundwater pumpingmodel for the exploration of water sources and could relieve the turbidity of the surface water through the filtration of riverbed. If the groundwater is pumping from the riverside, both the river and the aquifer could be recharge, and the reduce effect on the aquifer resulting from the exploration of groundwater could be relieved.
Maoluo River is a branch of theWu River, which is situated in the central part of the western coast of Taiwan. It is located to the east of the CentralMountain Range, to the north of the Tachia River basin, to the west of the Taiwan Strait, and to the south of the Zhuoshui River basin. The catchments incline from the northeast to the southwest. The trunk stream is 119.13 km long, and the drainage area is 2,025.6 km2. Fig. 1(a) shows the Wu River system and the research area is adjacent to Kuaiguan. Based on the geological data from the database of Central Geological Survey Institute (CGS, 2006)[4], the geologic profile from Fenyuan to Kuaiguan (A-A’ in Fig. 1(a)) is shown in Fig. 1(b). In the Fig. 1(b), except for Point A and A’, which are mainly composed of pebbles, most of the other points are composed of clay and fine sand. In the Kuaiguan area the surface is covered with few gravel, the lower part is mostly composed of sand.

The Kuaiguan region is of subtropical climate it has abundant rains but its rainfalls are not distributed evenly in the region or in terms of season. With respect to the time of rainfalls, May to October every year is the period when there are lots of typhoons and rainstorms, thus it is the wet season of the research area. October to April of the following year is the dry season. The average monthly rainfall is high from August to October, but little from January to February and the average annual rainfall is 1,000 to 2,000 mm. The distribution of groundwater level is affected by the terrain. It is obvious that the groundwater level descends from the east to the west. The annual mean temperature is 22.5℃. The annual average evapotranspiration is 900 to 1,200 mm. May to September is the wet season for river in Kuaiguan region, and the flow quantity in this period accounts for 70% of the whole year. January and February belongs to the dry season.

3 Analysis on optimization settings of single well pumping

In order to utilize the groundwater in a reasonable way, an appropriate standard for groundwater level should be prepared to achieve the sustainable pumping of water resources. Water Resources Agency (2007) was proposed the groundwater management index (GMI), that is set as one standard deviation (1sd) below the mean groundwater level is set as the lower limit of groundwater level, while double standard deviation (2sd) below was set as the lowest limit[22].
This research estimated the standard deviation and treated it as a standard for the limit of groundwater level based on the information of groundwater level from the 12 observation wells at the middle and upper reaches of the Wu River and the mean groundwater level from 2002 to 2004. The mean groundwater level is 35 m and the standard deviation is 1.04 m in the Kuaiguan region. Therefore, this research estimates that the lower and lowest limit of groundwater level is 33.96 and 32.92 m in the research area, respectively.
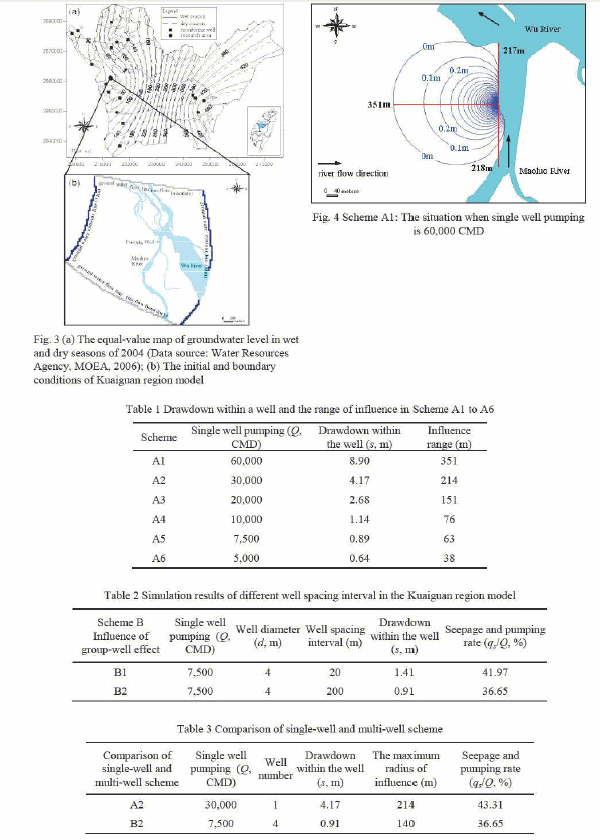
In this research, a wide-mounted well was used for pumping groundwater from the riverside. It is postulated that the diameter of well is 4 m, the distance from it to the river is 10 m, and the pumping time is 360 days. Scheme A1 to A6 simulated the effects of different pumping amount on the aquifer in the research area. The simulation results with Scheme A1 explain for the example and shown in Fig. 4. This scheme simulates the situation when single well pumping is 60,000 CMD. The drawdown within the well is 8.9 m, and the maximum radius of influence is 351 m. The drawdown within the well and the range of influence in Scheme A1 to A6 are shown in Table 1.


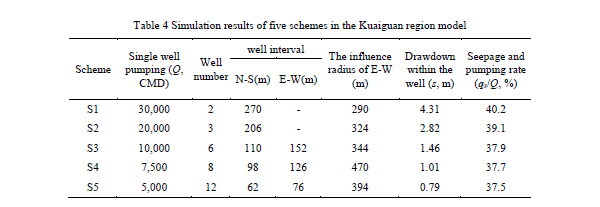
The simulation results of Scheme A in Table 1 indicate that the drawdown of groundwater level and its range of influence would decrease along with the reduction of pumping amount. If GMI is 1sd (s=1.04 m), the drawdown of groundwater level in Scheme A5 (s=0.89 m) and that of Scheme A6 (s=0.64m) shown in Table 1 conform to the restriction requirements. However, if GMI is 2sd (s=2.08 m), the Scheme A4 (s=1.14 m), A5, and A6 all conform to the restriction requirements.

4 Influence of group-well effect on the drawdown of groundwater level

When the space between two wells is shorter than the radius of influence, interference will appear in the drawdown of groundwater level and pumping amount, thus the interference is seen as the group-well effect (Xue 1986)[24]. In this research, Scheme B was made to explore whether the riverside groundwater pumping is influenced by the group-well effect or not. It is postulated that the pumping of the four wells are all 7,500 CMD, and they are located 10 m away from the river and parallel to the river. The simulation results of Scheme A5 indicate that when the pumping is 7,500 CMD, the radius of influence from the north to the south is about 50 m. Thus, it is postulated that Scheme B1 is influenced by the group-well effect, and the well spacing interval is set as 20 m. Scheme B2 simulates the situation where the exploited well is not influenced and the well spacing interval is set as 200 m. The simulation results of the drawdown of groundwater level and the radius of influence are shown in Table 2.
Scheme B1 simulates the situation where the exploited wells are influenced. The influence scope of the groundwater is 264 m from the east to the west and 257 m from the north to the south and the maximum drawdown is 1.41 m. Scheme B2 simulates the situation where the exploited wells are not influenced. The influence scope of the groundwater is 132 m from the east to the west and 140 m from the north to the south and the maximum drawdown is 0.91 m. The simulation results of Scheme B1 indicate that the influence scope and the drawdown within the wells are greater than those in Scheme B2.
In order to compare the situations with the same pumping but different quantity of wells, Schemes A2 and B2 are designed in this research to explore the distinction between single-well exploitation and multi-well exploitation, and the simulation results are shown in Table 3. In Scheme A2, there is only one well and the single well pumping is 30,000 CMD, while in Scheme B2, there are four wells, and the pumping of each well is 7,500 CMD. In terms of drawdown of groundwater level and radius of influence, the single-well scheme A2 has a greater effect than the multi-well scheme B2. Though Scheme B2 gives rise to less seepage than Scheme A2, it is applicable for the exploitation of water source owing to its small effect on the groundwater.

5 Assessment of appropriate groundwater pumping schemes

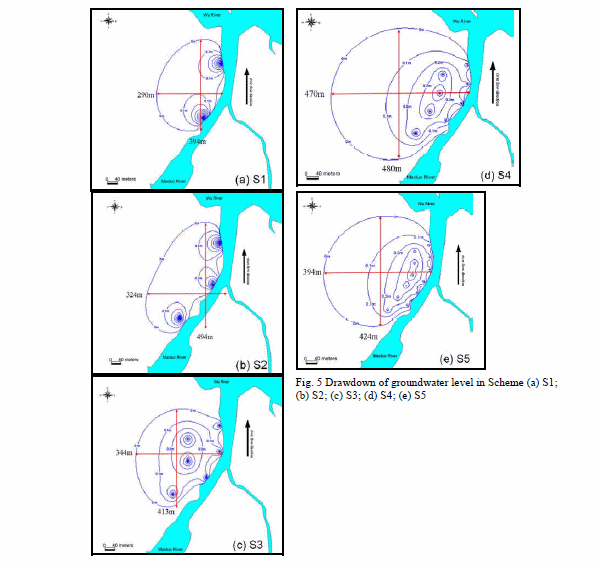
This research proposes five groundwater pumping schemes based on the assessment on the effect of different groundwater pumping, group-well effect, single-well and multi-well on the groundwater level; it also explores the effect of each scheme on the research area. The settings of each scheme are shown in Table 4, and the drawdown of each scheme is shown in Table 4 and Fig 5(a) to 5(e).
In Scheme 1, there are two pumping wells with equal pumping of 30,000 CMD. They are located parallel to the river with a well spacing interval of 270 m. After the drawdown of groundwater level becomes stable, the maximum drawdown within the wells is 4.31 m and the drawdown is shown in Fig 5(a). It is indicated from the drawdown of groundwater level in the figure that the influence scope of Scheme 1 is about 394 m from the north to the south and about 290 m from the east to the west, which mainly results from the spatial distribution of pumping wells. The Scheme 2 to Scheme 5 simulation results are show in Table 4 and Fig. 5(b) to 5(e), respectively.

6 Summary and Conclusion

This research explored the effect of riverside groundwater pumping on the river seepage. First of all, it verified the reliability of numerical model by using the groundwater flow software MODFLOW to construct the four analytical models proposed by Grigoryev (1957), Hantush (1965), Wilson (1993), and Hunt (1999). This research then constructed the numerical model for the groundwater flow in the Kuaiguan region in middle Taiwan, and explored the effect of riverside pumping on the seepage of the river in terms of hydrogeologic parameters and pumping well types.
The four analytical models are simulated by MODFLOW, and the verified results indicate that the riverside groundwater pumping could be simulated correctly. It is estimated that qs/Q is about 3.74% in the model where the river partially penetrates the aquifer, and it increases to 35.31% in the model where the river fully penetrates the aquifer. It is indicated that whether a river fully penetrate the aquifer is an important factor that affects the river seepage. If a river fully penetrates the aquifer, it is estimated that the qs/Q is 35.31%, while if there is a low permeable soil layer between the river and the aquifer, the qs/Q is 21.06%. It indicates that the low permeable soil layer in this model has an effect on qs/Q by 14.25%.
The sensitivity analysis results of hydrogeologic parameters based for the Maoluo River model indicate that the horizontal permeability coefficient (Kh), permeability coefficient of riverbed (K’), and the difference between the groundwater level and the river water level (x) are the important factors that may affect the mode. From the effect of pumping time, pumping amount, and qs/Q, it is indicated that qs/Q is about 42.7% and becomes stable 240 days later. When the pumping amount increases, the seepage of the river would be positively corrected to the drawdown of groundwater level.
The effect of pumping well diameter on qs/Q indicates that the increase of well diameter does not have a remarkable effect on the river seepage, but could result in drawdown of the groundwater level within the well. Therefore, the drawdown of groundwater could be controlled by adjusting the pumping well diameter. From the effect of the distance between the pumping well and the river, it is estimated that if the distance becomes bigger, qs/Q will decrease a little. The simulation results of each scheme indicate that the radius of influence from the east to the west is between 290 m and 470 m. From the top view of Fig. 9, it can be seen that the research area is about 700 m away from the residential area, thus none of the schemes will affect the residential area.
If the lower limit for drawdown of water level is set as 1.04 m, the drawdown in both Schemes 4 and 5 conform to the requirement. If the lowest limit is set as 2.08 m, all of Schemes 3, 4, and 5 will conform to the restriction requirement. From Fig. 10 is indicated that the qs/Q derived from Schemes 3, 4, and 5 is between 37.9% and 37.5%, and

Acknowledgment

This work was supported by the Ministry of Education, Taiwan, R.O.C. under the NCKU Project for Promoting Academic Excellence & Developing World Class Research Centers.

References

• Bochever F.M.: Evaluation of well-field yield in alluvial aquifers: The impact of a partially penetrating stream [C]. Proceedings of VODGEO (Hydrogeology) 13:84-115. (1966)
• Butler J.J., Zlotnik V.A., TsouM.S.: Drawdown and stream depletion produced by pumping in the vicinity of a partially penetrating stream. Ground Water 39(5): 651- 659. (2001)
• Central Geological Survey, MOEA, information on http://www.moeacgs.gov.tw/ (2006).
• ChenW.P., Lee C.H.: Estimating ground-water recharge from stream flow records. Environ Geol 44: 257-265. (2003)
• Chen J.W., Pan W.J., Lee C.H.: The groundwater of safe yield in Chou-Shui alluvial fan and Pingtung plane, Taiwan. Taiwan Water Conservancy 50(3):70-82 (2002), in Chinese.
• Chen J.W., Hsieh H.H., Yeh H.F. and Lee C.H.: The Effect of the Variation of River Water Level on the Estimation Groundwater Recharge in Hsinhuwei River, Taiwan, Environ Geol. DOI: 10.1007/s12665-009-0117-2. (2009)
• Chen X.H., Yin Y.: Semianalytical solution for stream depletion in partially penetrating streams. Ground Water 42(1):92-96. (2004)
• Chen X., Chen X.: Effect of aquifer anisotropic on the migration of lnfiltrated stream water to a pumping well. J Hydrol Eng 8(5):287-293. (2003)
• Glover R.E., Balmer C.G.: River depletion from pumping a well near a river. American Geophysical Union Transactions 35(3):468-470. (1954)
• Grigoryev V.M.: The effect of streambed siltation on well-field yield in alluvial aquifers. Water Supply and Sanitation 6:110-118. (1957)
• Hantush M.S.: Wells near streams with semipervious beds. J Geophysical Research 70(12):2829-2838. (1965)
• Hsieh H.H., Chen J.W., Lee C.H.: Analysis the quantity and quality of ground water for the riverside area. Water Supply Quarterly 26(3):1-10 (2007), in Chinese.
• Hunt B.: Unsteady stream depletion from ground water pumping. Ground Water 37(1):98-102. (1999)
• Jenkins C.T.: Techniques for computing rate and volume of stream depoetion by well. Ground Water 6(2):37-46. (1968)
• Lee C.H., ChenW.P., Lee C.H.: Estimation of groundwater recharge using water balance coupled with base-flow-record estimation and stable-base-flow analysis. Environ Geol 51(1):73-82. (2006)
• Matteo L.D., Dragoni W.: Empirical relationships for estimating stream depletion by a well pumping near a gaining stream. Ground Water 43(2):242-249. (2005)
• Theis C.V.: The effect of a well on the flow of a nearby stream. American Geophysical Union Transactions 22(3):734-738. (1941)
• Water Resources Agency,Ministry of Economic Affairs, information on http://gweb.wra.gov.tw/ (2007)
• Wilson J.L.: Induced infiltration in aquifer with ambient flow. Water Resour Res 29(10):3503-3512. (1993)
• Xue Y.: Ground water dynamics theorem. Geology publisher, Beijing (1986), in Chinese.